Revolutionäre Rechnungen
Wie kann die wissenschaftliche Qualität der Arbeit eines Forschers objektiv gemessen werden? Sune Lehmann, dänischer Physiker und Weinliebhaber, vergleicht einzelne Forscher miteinander und stellt in Nature seinen Lösungsvorschlag für das Problem vor.

(07.02.2007) Wenn etwas die Forschung revolutionieren würde, dann ein objektives, leicht bestimmbares quantitatives Maß für die wissenschaftliche Qualität der Arbeit eines Forschers. Dies aus zwei Gründen: Zum einen wäre es ein ungeheurer Ansporn für den Nachwuchs, an seiner tatsächlichen Leistung gemessen zu werden, und nicht mehr abzuhängen von den Sympathien, Vorurteilen und Launen ihrer Chefs und Gutachter und unvorhersagbaren und unbeeinflussbaren politischen Konstellationen. Des weiteren würde sich das kafkaeske Antrags- und Begutachtungssystem in das auflösen, was es im Grunde ist: heiße Luft.
Gibt es ein quantitatives Maß für die wissenschaftliche Qualität der Arbeit eines Forschers?
In der von dem Budapester Tibor Braun herausgegebenen Zeitschrift
Scientometrics findet sich in Band 67, S. 491-502, der Artikel von Anthony van Raan:
Comparison of the Hirsch-index with standard bibliometric indicators and with peer judgement for 147 chemistry research groups. Darin untersucht Raan zwar keine einzelnen Forscher sondern Forschungsgruppen, er vergleicht aber unter anderem folgende Qualitätsindikatoren:
1. Den
Hirsch-Index. Dazu erfasst man die zu bewertenden Publikationen eines Forschers und sortiert sie nach der Häufigkeit der Zitierungen. Der Hirsch-Index ist die Zahl, bei der die Anzahl der Zitierungen gerade noch größer als die Rangnummer des betreffenden Artikels ist oder bestenfalls gleich groß. Ein Hirsch-Index von beispielsweise vierzig bedeutet, dass von allen Arbeiten eines Forschers vierzig Artikel mindestens vierzigmal zitiert wurden. (Informationsvermittlungsstelle der MPG)
2. Die
Zahl der Publikationen im Science Citation Index aufgeführter Journale.
3. Die
Zahl der erhaltenen Zitationen (ohne Selbstzitationen).
4. Die
durchschnittliche Zahl von Zitationen pro Paper (ohne Selbstzitationen), bezogen auf alle Veröffentlichungen eines Autors.
5. Die durchschnittliche Zahl von Zitationen pro Paper (ohne Selbstzitationen) bezogen auf die durchschnittliche Zahl von Zitationen pro Paper des Fachgebietes. Diesen Indikator nennt van Raan
Kronen-Indikator.
6. Die
Noten, die eine Reihe von Gutachtern der betreffenden Forschungsgruppe erteilt hat.
In Raans Indizes fließen nur Forschungspaper ein, also keine Reviews und Buchbeiträge. Die Größe der Forschungsgruppe und die ihr zur Verfügung stehenden Geldmittel wurden nicht berücksichtigt. Raan kommt zu dem Schluss, dass sowohl der Hirsch-Index als auch der Kronen-Index etwa die gleiche Urteilskraft haben, beziehungsweise zum gleichen Urteil kommen, wie ein Panel von Gutachtern.
Einzelne Forscher verglichen der dänische Rotweinliebhaber Sune Lehmann und seine Kollegen Andrew D. Jackson und Benny Lautrup. Ihre Erkenntnisse schienen
Nature wertvoll genug, um sie als Titelgeschichte zu veröffentlichen (
"Measures for measures" in
Nature 444, S. 1003-1004). Die Physiker gingen von dem Gedanken aus, dass ein Maß für die Leistung eines Forschers vor allem ein Kriterium erfüllen müsse: Es muss dem Forscher mit Sicherheit zuordenbar sein, ihn quasi charakterisieren.
Lehmann, Jackson und Lautrup untersuchten drei Indikatoren: die durchschnittliche Zahl von Zitationen pro Paper, die Zahl der in einem Jahr publizierten Paper und den Hirsch-Index. Da nur die Forscher eines engen Arbeitsgebiets, der Hochenergiephysik, verglichen wurden, dürfte die durchschnittliche Zahl der Zitationen pro Paper das gleiche messen wie der Kronen-Index von Raan. Auch hier wurden (richtigerweise) keine Reviews oder Buchbeiträge berücksichtigt.
Wie gingen Lehmann und sein Team vor?
Zuerst ordneten sie die Forscher nach Maßgabe der drei Indikatoren, und zusammen mit der Liste nach ihren Anfangsbuchstaben geordneter Forscher erhielten sie vier Listen: eine alphabetische Liste, Papers pro Jahr, h-Index sowie die durchschnittliche Zahl von Zitationen pro Paper (siehe
Abbildung unten). Der Einfachheit halber packten sie für jede Liste die Forscher in zehn Ranggruppen zusammen. Auf diese Ranggruppenlisten wurde die Wahrscheinlichkeitsrechnung angewendet. Vermutlich deswegen fand der Artikel in der mathephoben Biologenwelt nicht den Widerhall, den er verdient.
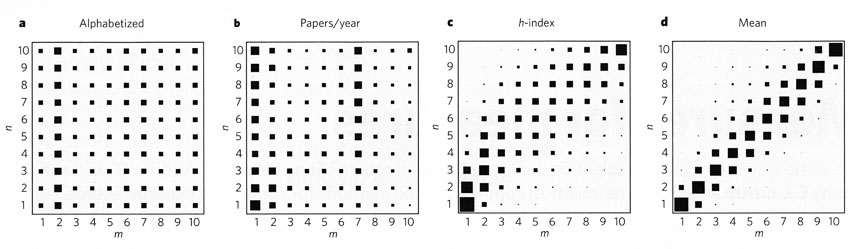
Dieses Vorgehen ist allerdings auch nicht ganz trivial: Anhand der vollständigen Zitationsgeschichte eines Forschers aus Ranggruppe n wird so die bedingte Wahrscheinlichkeit berechnet, dass eines der Paper des Forschers k Zitationen erhält. Damit wiederum und mit dem Bayes-Theorem berechneten die drei Physiker die bedingte Wahrscheinlichkeit, dass der Forscher in Ranggruppe m kommt. Für jede Liste gibt es zu jedem Paar m/n also eine Wahrscheinlichkeit. Trägt man m gegen n auf und versinnbildlicht die Wahrscheinlichkeiten durch unterschiedlich dicke Quadrate, erhält man für jede Liste, das heißt für jeden Indikator, eine Verteilung der Wahrscheinlichkeiten. Im Fall eines idealen Indikators würden die Wahrscheinlichkeiten in der Diagonale 1 und im Rest des Feldes 0 sein. Das heißt: An der ursprünglichen Einordnung in Ranggruppe n ändert sich nichts, die Einordnung ist klar und eindeutig.
Wie sieht es nun mit den vier Indikatoren beziehungsweise Listen aus? Bei Ranganordnung nach dem Alphabet (diese Liste dient als eine Art Negativ-Kontrolle, da sie völlig beliebig ist) verteilen sich die Wahrscheinlichkeiten gleichmäßig über das ganze Feld. Mit anderen Worten: Der Nachname eines Forschers sagt nichts über die Qualität seiner Forschung aus.
Erstaunlicherweise gilt mehr oder weniger das gleiche für den Indikator Paper/Jahr, die Wahrscheinlichkeitsverteilung streut auch hier über das ganze Feld. Lehmann daher:
"The best that can be said of publication frequency is that it measures industry rather than ability."
Beim Hirsch-Index (h-Index) konzentrieren sich die Wahrscheinlichkeiten auf die Mitte des m/n-Diagramms, jedoch mit großer Unschärfe, und zudem ergibt sich eine gebogene Kurve – warum, wird nicht näher erläutert. Lehmann hält den Hirsch-Index für einen schlechten Qualitäts-Indikator – allerdings für besser als die Zahl der Paper pro Jahr.
Beim Indikator "mittlere Zitate pro Paper" konzentrieren sich die Wahrscheinlichkeiten in der Diagonale des m/n-Diagramms. Die mittleren Zitate pro Paper seien also der beste Qualitäts-Indikator, so Lehmann.
Das zu glauben ist nicht jedermanns Sache. Die Arbeit von Lehmann und Co. stieß unter anderem auf den Widerspruch von Boris Egloff von der Universität Leipzig. Er glaubt (und begründet das), dass Lehmann teilweise einem Zirkelschluss zum Opfer gefallen sei: Er habe die Zahl von Zitationen benützt, um ein Maß zu bestätigen, das ebenfalls aus Zitationen gewonnen wurde. Man müsse die Gültigkeit der Indikatoren jedoch durch unabhängige Messungen bestätigen.
Des weiteren schreibt Egloff, dass wenn man die Forscher an der durchschnittlichen Zahl der Zitationen ihrer Publikationen messe, der Ausstoß an Papern zurückginge. Die Forscher würden nicht mehr in Salami-Taktik publizieren, sondern nur noch bedeutende Ergebnisse, weil sonst ihr Zitationsschnitt abnähme. Das allerdings sei ein wünschenswerter Effekt des Lehmannschen Indikators.
Bei letzterem übersieht Egloff allerdings, dass die Zuverlässigkeit des Lehmannschen Indikators von der Zahl der Paper eines Forscher abhängt. Für eine Zuverlässigkeit von neunzig Prozent sind etwa fünfzig Paper erforderlich. Es genügt also nicht, zwei bis drei gut zitierte Paper zu veröffentlichen und sich dann zur Ruhe zu setzen: Die mittlere Zahl von Zitationen pro Paper wäre einfach zu unsicher.
Was ebenfalls für Lehmanns Indikator spricht, ist Raans Befund, dass das Urteil von Gutachtern mit dem Kronen-Index einigermaßen übereinstimmt. Der Kronen-Index ist vergleichbar mit Lehmanns Index und die Gutachterbeurteilung wäre das von Egloff geforderte unabhängige Kriterium.
Siegfried Bär
Wahrscheinlichkeitsverteilung von vier Indikatoren nach Lehmann:
die horizontalen Reihen zeigen die Wahrscheinlichkeiten, dass ein Autor,
der ursprünglich in die Ranggruppe n eingeordnet war, auch in Ranggruppe
m auftaucht. Die Wahrscheinlichkeiten sind proportional zur Größe der
Quadrate.
a Forscher alphabetisch aufgelistet;
b Zahl der
in einem Jahr publizierten Paper;
c Hirsch-Index (h-Index);
d durchschnittliche Zahl von Zitationen pro Paper. (aus
Nature 444, 21/28.12.2006, S.1003-1004)
Letzte Änderungen: 12.02.2007





 (07.02.2007) Wenn etwas die Forschung revolutionieren würde, dann ein objektives, leicht bestimmbares quantitatives Maß für die wissenschaftliche Qualität der Arbeit eines Forschers. Dies aus zwei Gründen: Zum einen wäre es ein ungeheurer Ansporn für den Nachwuchs, an seiner tatsächlichen Leistung gemessen zu werden, und nicht mehr abzuhängen von den Sympathien, Vorurteilen und Launen ihrer Chefs und Gutachter und unvorhersagbaren und unbeeinflussbaren politischen Konstellationen. Des weiteren würde sich das kafkaeske Antrags- und Begutachtungssystem in das auflösen, was es im Grunde ist: heiße Luft.
(07.02.2007) Wenn etwas die Forschung revolutionieren würde, dann ein objektives, leicht bestimmbares quantitatives Maß für die wissenschaftliche Qualität der Arbeit eines Forschers. Dies aus zwei Gründen: Zum einen wäre es ein ungeheurer Ansporn für den Nachwuchs, an seiner tatsächlichen Leistung gemessen zu werden, und nicht mehr abzuhängen von den Sympathien, Vorurteilen und Launen ihrer Chefs und Gutachter und unvorhersagbaren und unbeeinflussbaren politischen Konstellationen. Des weiteren würde sich das kafkaeske Antrags- und Begutachtungssystem in das auflösen, was es im Grunde ist: heiße Luft.